Szetho.com

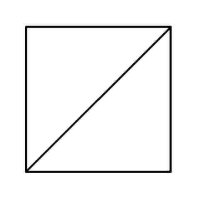
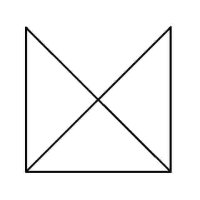
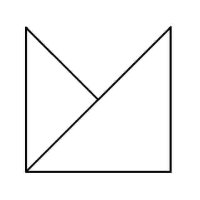
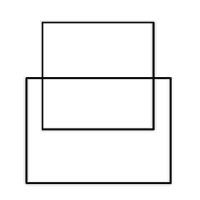
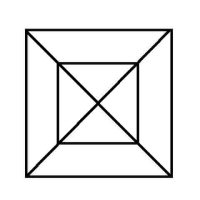
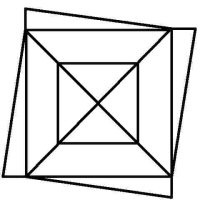
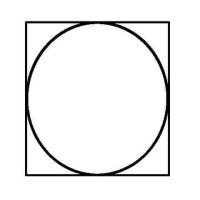
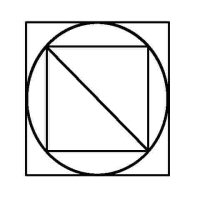
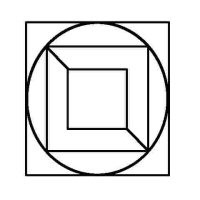
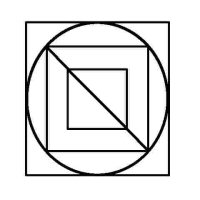
We've all seen these geometric puzzles which challenge you to trace along all of the lines, without lifting the pen from the paper and tracing each line only once. How many of these puzzles can you complete? How many of these puzzles are possible and how many are impossible? Is there a way of knowing whether a puzzle of this sort is possible without trying it? There is. Try them first and then check the answers, as well as learn the secret.

When you know the Euler's Rule it's easy to make up your own puzzles like these, and be confident of whether they are possible or not - all you need is a pen and a flip-chart: great for coffee break diversions, team building exercises, etc.

Puzzle 1 - Easy ones first?......
Puzzle 2 - Still easy? Can it be done?....
Puzzle 3 - Looks easy, but not so easy. Can it be done?
Puzzle 4 - Now this one is easy...
Puzzle 5 - Easy.
Puzzle 6 - Easy.
Puzzle 7 - Looks very difficult. Can it be done?
Puzzle 8 - Don't even try this one...
Puzzle 9 - It's got something to do with where you start...
Puzzle 10 - Same applies here - where you start makes all the difference - assuming it can be done...
Puzzle 11 - Like I said, assuming it can be done...
Puzzle 12 - It would be a pity to end with one that's impossible...

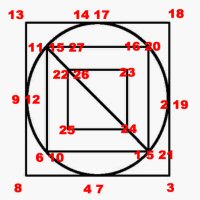
Euler puzzles are named after the man who devised the method of knowing if they are possible or not. Leonhard Euler was a brilliant 18th century mathematician who solved the puzzle of the Konigsberg bridges (now Kaliningrad, in Russia). Seven bridges connected both sides of the city and two islands in between. The townsfolk passed their time for many years trying (unsuccessfully) to find a route which would cross each bridge only once. Euler proved that is was not possible, until an eighth bridge was constructed (unfortunately little remains of the original city or its bridges since the 2nd World War). Nevertheless Euler's Rule survives, and is now used in planning routes and service territories (for postal services, meter reading, door-to-door deliveries, etc) the world over, to eliminate unnecessary travel and back-tracking. So what's the secret?

Impossible are 3, 7, 8 and 11. The others are all possible. Here is the secret for knowing virtually at a glance whether a puzzle like this is possible: (This is 'Euler's Rule') - the points at which lines cross or connect are called nodes. A node with an odd number of connecting lines is called an 'odd node'. An odd node is therefore a connecting or crossing point for 3, 5, 7, etc, lines. For a puzzle to be possible it must have two or no odd nodes. In other words, any puzzle with one odd node, or more than two odd nodes, is impossible. Added to which, to complete a puzzle with two odd nodes, you must begin it at one of the odd nodes and end at the other, or the puzzle cannot be completed. Now go back and try the ones you couldn't do first time, and think about what little changes could be made to the impossible puzzles to make them possible (an example is the change from puzzle 11 to puzzle 12). In Konigsberg, the bridges were effectively the lines and the river banks and islands were the nodes. The seven bridge puzzle was impossible because there were four odd nodes. The eighth bridge turned two of those odd nodes into even nodes, leaving two odd nodes and a puzzle which could then be solved.

Below is a solution to the Euler puzzle 12, if you need it, which should help you solve the others too.

Try to work it out for yourself first using the rules above (i.e., start at one odd node, and finish at the other) before resorting to the full answer.

Obviously start at point 1, which is the odd node, bottom-right, then go to 2, then 3, and so on, finishing at point 27, the other odd node, top-left.